A Local Fourier Slice Equation
Christian Lessig
Optics Express 2018, Vol. 26, Issue 23, pp. 29769-29783 (2018).
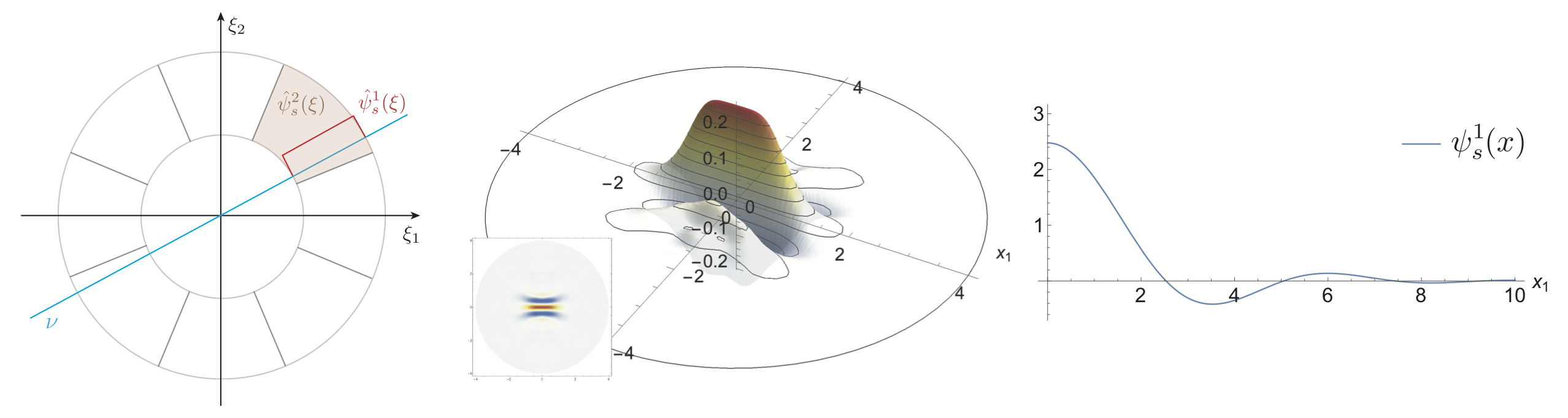
Left: Conceptual depiction of our construction. Middle and right: Directional polar wavelet in two dimensions (middle) and its ``sliced'' counter-part btained by projecting along the x_2-axis (right).
We present a local Fourier slice equation that enables local and sparse projection of a signal. Our result exploits that a slice in frequency space is an iso-parameter set in spherical coordinates. The projection of suitable wavelets defined separably in these coordinates can therefore be computed analytically, yielding a sequence of wavelets closed under projection. Our local Fourier slice equation then realizes projection as reconstruction with "sliced" wavelets with computational costs that scale linearly in the complexity of the projected signal. We numerically evaluate the performance of our local Fourier slice equation for synthetic test data and tomographic reconstruction, demonstrating that locality and sparsity can significantly reduce computation times and memory requirements.