PsiEC: A Local Spectral Exterior Calculus
Christian Lessig
Applied and Computational Harmonic Analysis, 51:56–103, March 2021
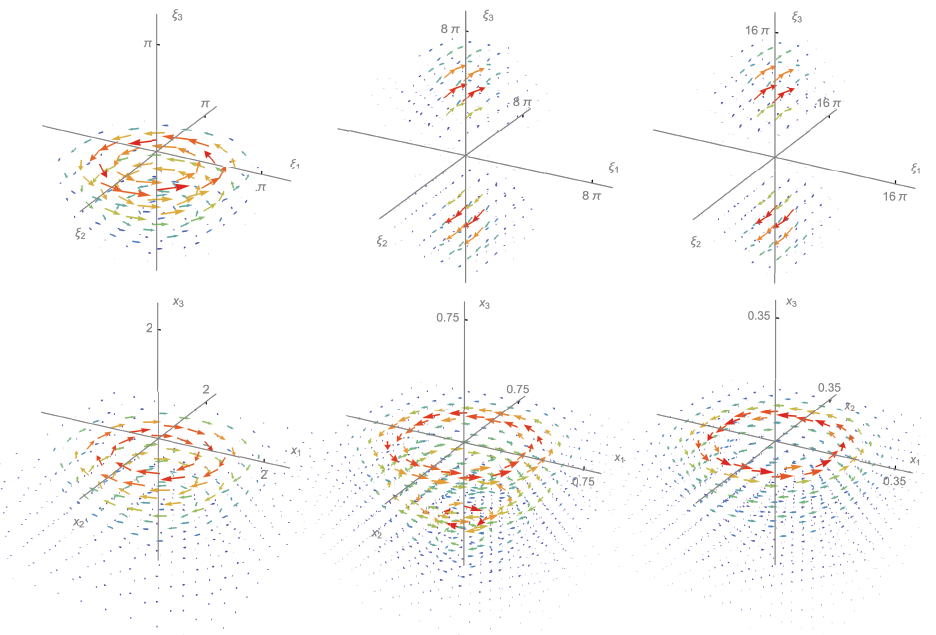
Exact differential 2-form basis functions in 3D with different angular localization in the Fourier domain (top) and the spatial domain (bottom) visualized as vector fields.
We introduce PsiEC, a discretization of Cartan's exterior calculus of differential forms using wavelets. Our construction consists of differential r-form wavelets with flexible directional localization that provide tight frames for the spaces of r-forms in R^2 and R^3. By construction, the wavelets satisfy the de Rahm co-chain complex, the Hodge decomposition, and that the k-dimensional integral of an r-form is an (r−k)-form. They also verify Stokes' theorem for differential forms, with the most efficient finite dimensional approximation attained using directionally localized, curvelet- or ridgelet-like forms. The construction of Ψec builds on the geometric simplicity of the exterior calculus in the Fourier domain. We establish this structure by extending existing results on the Fourier transform of differential forms to a frequency description of the exterior calculus, including, for example, a Plancherel theorem for forms and a description of the symbols of all important operators.
Resources
title = "PsiEC: A local spectral exterior calculus",
journal = "Applied and Computational Harmonic Analysis",
volume = "51",
pages = "56 - 103",
year = "2021",
issn = "1063-5203",
doi = "https://doi.org/10.1016/j.acha.2020.10.003",
url = "http://www.sciencedirect.com/science/article/pii/S1063520320300737",
author = "Christian Lessig",}