Divergence Free Polar Wavelets for the Analysis and Representation of Fluid Flows
Christian Lessig
Journal of Mathematical Fluid Mechanics 2019.
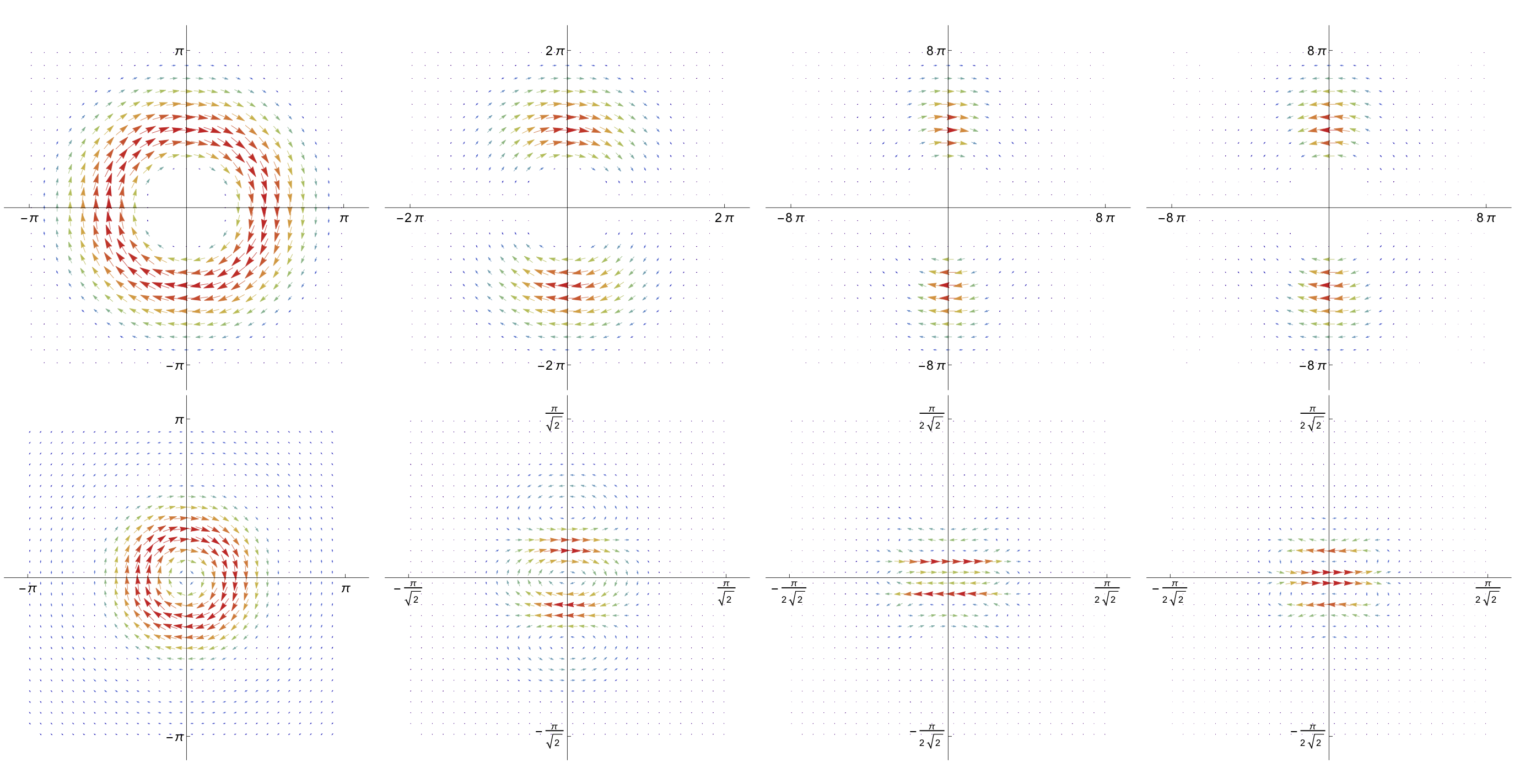
Our divergence free wavelets in the frequency (top) and spatial (bottom) domains. Using a definition of the wavelets in polar coordinates in the frequency domains allows for ideal divergence freedom while also enabling directional localization, e.g. to model the flow along boundaries of the flow domain or in the wake behind an object.
We present a Parseval tight wavelet frame for the representation and analysis of velocity vector fields of incompressible fluids. Our wavelets have closed form expressions in the frequency and spatial domains, are divergence free in the ideal, analytic sense, have a multi-resolution structure and fast transforms, and an intuitive correspondence to common flow phenomena. Our construction also allows for well defined directional selectivity, e.g. to model the behavior of divergence free vector fields in the vicinity of boundaries or to represent highly directional features like in a von Karrman vortex street. We demonstrate the practicality and efficiency of our construction by analyzing the representation of different divergence free vector fields in our wavelets.
Resources
- Read only access (no subscription required)
- Preprint
- Reference implementation (Mathematica)
- Presentation about the construction (given at Sandlab at MIT)