An Implementation of the MRRR Algorithm on a Data-Parallel Coprocessor

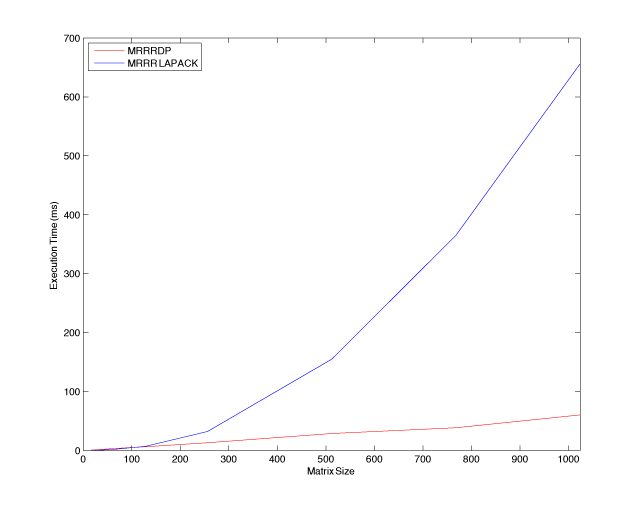
An Implementation of the MRRR Algorithm on a

Data-Parallel Coprocessor


Figure 1: Performance of the MRRR algorithm for random input matrices. MRRR DP is our implementation for data-parallel coprocessors, MRRR LAPACK is LAPACK's implementation.

Abstract: The eigenvalues and eigenvectors of a symmetric matrix are of interest in a myriad of applications. One of the fastest and most accurate numerical techniques for the eigendecomposition is the Algorithm of Multiple Relatively Robust Representations (MRRR), the first stable algorithm that computes the eigenvalues and eigenvectors of a tridiagonal symmetric matrix in O(n^2) arithmetic operations. In this paper we present a parallelization of the MRRR algorithm for data parallel coprocessors using the CUDA programming environment. The results demonstrate the potential of data-parallel coprocessors for scientific computations: compared to routine sstemr, LAPACK's implementation of MRRR, our parallel algorithm provides 10-fold speedups.

Publications

Christian Lessig and Paolo Bientenisi, On Parallelizing the MRRR Algorithm for Data-Parallel Coprocessors, To be presented at PPAM 2009, Eight International Conference on Parallel Processing and Applied Mathematics, Wroclaw, Poland, September 2009. (pdf, slides, bibtex)

Technical Report

Note that the following reports corresponds to an older version of our implementation.

Christian Lessig, An Implementation of the MRRR Algorithm on a Data-Parallel Coprocessor, Technical Report, University of Toronto, 2008. (pdf, bibtex)

September 2009